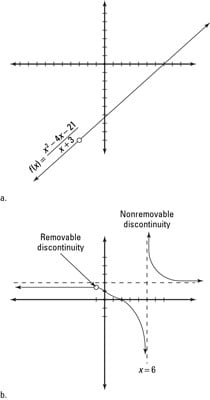
Redefine f(x) so that the function is continuous at that point.
Lim xa f (x) does not exist. There are three basic types of discontinuities: A removable discontinuity occurs when there is a rational expression with common factors in the numerator and denominator. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. Similarly, calculus in maths, a function f(x) is continuous at x = c, if there is no break in the graph of the given function at the point.

(removable type of discontinuities) in case, limit ₓ→ c f(x) exists but is not equal to f (c) then the function is said to have a removable discontnuity or discontinuity of the first kind.
The zeros at x = 3 (after a partial cancellation of one of two copies) and at x =7 remain. Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote. Continuity section 2 3 find points. In either of these two cases the limit can be quantified and the gap can be removed; removable discontinuities are those where there is a hole in the graph as there is in this case. A jump discontinuity at a point has limits that exist, but it's different on both sides of the gap. Since the function is a composition involving a trigonometric and rational functions, it is continuous on all points in its domain. (or swath of holes) in the graph of the function that could be filled (or a singleton point that can be moved/redefined) so as to make the function continuous there. There are three basic types of discontinuities: There is a gap at that location when you are looking at the graph. The function is continuous everywhere except one point for example, g (x) = sin(x) and h 1−cos x x are defined for x = 0, but x both functions have removable discontinuities. Here at max any one of the l.h.l or r.h.l can may be equal to f(a). However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point.
Until this point, our main focus was limits and how to determine them. This kind of discontinuity is known as removable discontinuity as illustrated in image also. 0 f(x) = −x x ≥ 0 this discontinuous function is seen in fig. A removable discontinuity exists when the limit of the function exists, but one or both of the other two conditions is not met. However, not all functions are continuous.

But their common value is not equal to f(a).
A removable discontinuity exists when the limit of the function exists, but one or both of the other two conditions is not met. There are several types of behaviors that lead to discontinuities. Graph of the discontinuous function listed below x +1 x > The functions that are not continuous can present different types of discontinuities. This function will satisfy condition #2 (limit exists) but fail condition #3 (limit does not equal function value). A removable discontinuity occurs when there is a rational expression with common factors in the numerator and denominator. I can calculate the needed function value to retain a limit and create continuity. The function is continuous everywhere except one point for example, g (x) = sin(x) and h 1−cos x x are defined for x = 0, but x both functions have removable discontinuities. The graph of f (x) stops and then begins again with an open circle at a different range value for a given value of the domain. Resourcefunction "functiondiscontinuities" takes the option "excluderemovablesingularities", having default value false, that determines whether to exclude removable discontinuities from the result.a function f(x) is said to have a removable discontinuity at a point x = a if the limit of f(x) as x → a exists and is independent of the direction in which the limit is taken, but has a value. However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point. From this example we can get a quick "working" The term removable discontinuity is sometimes incorrectly used for cases in which the limits in both directions exist and are equal, while the function is undefined at the point.
Tap again to see term 👆. I can locate removable discontinuities by using the definitions of limits and continuity. We've already seen one example of a function with a jump discontinuity: F(a) could either be defined or redefined so that the new function is continuous at r= a. Continuity section 2 3 find points.

(or swath of holes) in the graph of the function that could be filled (or a singleton point that can be moved/redefined) so as to make the function continuous there.
A jump discontinuity at a point has limits that exist, but it's different on both sides of the gap. However, a large part in finding and determining limits is knowing whether or not the function is continuous at a certain point. A removable discontinuity occurs when there is a rational expression with common factors in the numerator and denominator. I can locate removable discontinuities by using the definitions of limits and continuity. Avoidable, jump and essential discontinuity. When a rational function has a vertical asymptote as a result of the denominator being equal to zero at some point, it will have an infinite discontinuity at that point. Types of discontinuities (i) removable (ii) jump (iii) infinite nonremovable at a particular point we can classify three types of discontinuities. Does in fact have an official definition. If a function is not continuous at a point in its domain, one says that it has a discontinuity there. removable discontinuity hole a hole in a graph. I can calculate the needed function value to retain a limit and create continuity. There is a gap at that location when you are looking at the graph. Let's call this mathf(x) = \frac{\sin x}{x}/math.
Get Point Removable Discontinuity Definition Images. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. removable discontinuities are those where there is a hole in the graph as there is in this case. Therefore, x = 3 and x =7 are both infinite discontinuities of h, as well as the locations of vertical asymptotes on the graph of h. In either of these two cases the limit can be quantified and the gap can be removed; If a function is not continuous at x = a, but the limit of the function at x = a exists, then f(x) has a removable discontinuity.