The function f (x) will be discontinuous at x = a in either of the following situations and it has the following types of discontinuities discusses below :
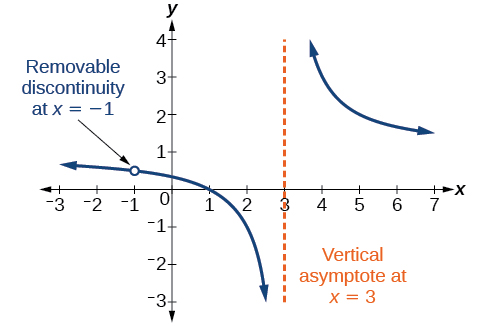
A point of discontinuity occurs when a number is both a zero of the numerator and denominator. Imagine you're walking down the road, and someone has removed a manhole cover. The factor that cancels represents the removable discontinuity. The graph has a hole, which you can see in figure a. In most cases, we should look for a discontinuity at the point where a piecewise defined function changes its formula.

Be sure they realize there is discontinuity where.
+ e x y = 0. 3 ( ) x f x d. discontinuity is removable, find a function g that agrees with f for a and is continuous at a. 3) identify the removable discontinuities if any. Direct students to compare and contrast the functions algebraically and. This fact can often be used to compute the limit of a continuous function. Discuss the continuity of the function f(x) = sin x. removable discontinuities of rational functions. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. Let us examine where f has a discontinuity. Let f(x) = p x 5 1 x +3, so that f(x) = 0 if and only if x is a solution to the equation. A function has a removable discontinuity at a if the limit as x approaches a exists, but either f(a) is different from the limit or f(a) does not exist. The roots of the equation in step 2 is where the removable discontinuity occurs.
• a point of discontinuity of a function f is a point in the domain. Determine if the graph has any holes/removable discontinuities. This fact can often be used to compute the limit of a continuous function. In most cases, we should look for a discontinuity at the point where a piecewise defined function changes its formula. removable discontinuity recall that last day we found lim x!0 x 2 sin(1=x) using the squeeze theorem.

This usually only happens when the given function is rational.
Identify asymptotic discontinuities (also known as infinite discontinuities) and removable discontinuities in a rational function and describe why these discontinuities exist. An essential discontinuity (also called second type or irremovable discontinuity) is a discontinuity that jumps wildly as it gets closer to the limit. These are the singular points for the equation. + e x y = 0. A single point where the graph is not defined, indicated by an open circle. removable and nonremovable discontinuities describe the difference between a discontinuity that is removable and a discontinuity that is nonremovable. The vertical asymptote occurs at x = − 2 because the factor x + 2 does not cancel. We call such a hole a removable discontinuity. discontinuity) and perform any calculations on the function. Of the numerator and the denominator. The function is defined for all x in the interval ( 0, ∞). This function will satisfy condition #2 (limit exists) but fail condition #3 (limit does not equal function value). The function f (x) has a discontinuity of the first kind at x = a if.
A point of discontinuity occurs when a number is both a zero of the numerator and denominator. A removable discontinuity is a discontinuity where the left hand and right hand limits of a function equal the same value while the function itself has a different value. First test at x = 0. Trace the graph with your finger, exaggerating the point of discontinuity. F(x)={(x^2 if x<1),(x if 1 le x <

Earlier, you were asked what happens to the equation \(\
These are the singular points for the equation. The factor that cancels represents the removable discontinuity. Identify asymptotic discontinuities (also known as infinite discontinuities) and removable discontinuities in a rational function and describe why these discontinuities exist. Both have a removable discontinuity at x 0. Evaluating f at 5 and at 6, we see that f(5) = p 5 5 1 5 +3 = 1 8 < F x = x + 1 x − 1 x + 1 x. Find the points of discontinuity of the function f (x) = arctan 1 x if they exist. + e x y = 0. The example problems are taken from hallale (1998). Let us examine where f has a discontinuity. First, however, we will define a discontinuous function as any function that does not satisfy the definition of continuity. The vertical asymptote occurs at x = − 2 because the factor x + 2 does not cancel. Features of rational functions and graphing rational functions.
44+ Removable Discontinuity Example Equation Pics. This is because the graph has a hole in it. Set the deno = 0 and solve. They are usually undefined and are represented by a hole or small circle in the graph. We can find the point by evaluating the function. The example problems are taken from hallale (1998).
We call such a hole a removable discontinuity removable discontinuity example. A discontinuity is removable if the limit of f(x) as x approaches x 0 from the left is equal to the limit as x approaches x 0 from the right, but this value is not equal to f(x 0).