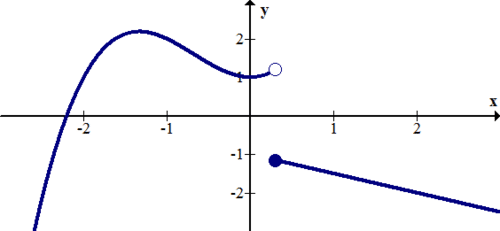
If a term doesn't cancel, the discontinuity at this x value corresponding to this term for which the denominator is zero is nonremovable, and the graph has a vertical asymptote.
The function is not continuous because there is a hole.in this case, all limits exist. Consider the function = {< non removable discontinuity the limit of the function does not exist 1. Continuity and discontinuity types of discontinuity b. B the function 𝑓 does not have a discontinuity at 𝑥 = − 3.

There are two ways a removable discontinuity is created.
A the function 𝑓 has a removable discontinuity at 𝑥 = − 3. If the discontinuity cannot be taken away. Lim xtc discontinuities can either be removable or non removable. The next step would be to check if these factors also appear in. Den fcx) = +16) a function is continuous on an olan interval (a,b) when the function is continuous for every point on the interval. Say for example the game is super mario bros, and jumping in a particular pixel will let you beat the stage in 10 seconds, while missing the jump will let you beat it in 20s. Each discontinuity can be characterized using limits, as follows. Other than that the rational function can have any other factors you want. Suppose you have two polynomials in a fraction: This is the currently selected item. D the function 𝑓 has an infinite discontinuity at 𝑥 = − 3. A value for the function. A discontinuity at c is called removable if f can be made continuous by appropriately defining (or redefining) for instance, the function in example 2(b) has a removable discontinuity at to remove the discontinuity, all you need to do is redefine the function so that
A removable discontinuity has a gap that can easily be filled in, because the limit is the same on both sides. Discontinuities that can't be removed are called irremovable, or essential; A discontinuity at c is called removable if f can be made continuous by appropriately defining (or redefining) f(c). A function with a nonremovable discontinuity at x — 2. discontinuity of a rational function occurs when its denominator is zero.

Then give an example of a function that satisfies each description.
In your explanation, give examples of the following descriptions.(a) a function with a nonremovable discontinuity at x = 4(b) a function with a removable discontinuity at x = −4(c) a function that has both of the. In your explanation, give examples of the following descriptions: discontinuity of a rational function occurs when its denominator is zero. removable and nonremovable discontinuities describe the difference between a discontinuity that is removable and one that is nonremovable. Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. Say for example the game is super mario bros, and jumping in a particular pixel will let you beat the stage in 10 seconds, while missing the jump will let you beat it in 20s. Touch device users, explore by touch or with. The function is continuous.in this case, all the limits exist. In the graph at x = a. This is the currently selected item. A removable discontinuity is sometimes called a point discontinuity, because the function isn't defined at a single (miniscule point). (c) a function that has both of the characteristics described in. There are two types of.
Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. In your explanation, give examples of the following descriptions: 2 🔴 on a question describe a place on earth that would not be considered part of the biosphere. Continuity and discontinuity types of discontinuity b. A removable discontinuity is a point on the graph that is undefined or does not fit… random posts 4 ways to help a college student prepare for the first semester
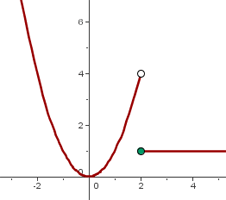
The function is not continuous because there is a jump or because there is an infinite portion which leads to an asymptote.
This singularity can be removed by defining. non removable discontinuity the limit of the function does not exist 1. Infinite discontinuity the function doesn't approach a particular finite value, the limit does not exist. 2 🔴 on a question describe a place on earth that would not be considered part of the biosphere. This is the currently selected item. The graph of a removable discontinuity leaves you feeling empty, whereas a graph of a nonremovable discontinuity leaves you feeling jumpy. A) a function with a nonremovable discontinuity at x=4. Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. A function continuous on the interval 600,00) is everywhere continuous. The functions are rational, linear with a hole, and piecewise. In your explanation, give examples of the following descriptions: (a) a function with a nonremovable discontinuity at x = 4. Discontinuities fall into two categories:removable and nonremovable.
Download Removable And Nonremovable Discontinuity Examples PNG. One way is by defining a blip in the function and the other way is by the function having a common factor in both the numerator and denominator. The next step would be to check if these factors also appear in. "fill in the hole, or erase the point and move it to the hole." The graph will have a vertical asymptote. C the function 𝑓 has a jump discontinuity at 𝑥 = − 3.
Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r removable discontinuity example. Continuity of a function example