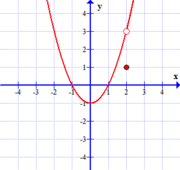
removable discontinuities can be "fixed"
removable discontinuities are characterized by the fact that the limit exists. These holes are called removable discontinuities. The other types of discontinuities are characterized by the fact that the limit does not exist. removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. removable discontinuities can be "fixed"

In the next section, we will solve some examples in which we will find the removable discontinuity of a function and plot it on the graph.
If a function is not continuous at x = a, but the limit of the function at x = a exists, then f(x) has a removable discontinuity. Occasionally, a graph will contain a hole: But the value at x = 0 is undefined. In the graphs below, there is a hole in the function at x=a. In this example, both and + don't exist, thus satisfying the condition of essential discontinuity. In particular, the above definition allows one only to talk about a. Below is the graph for f ( x) = ( x + 2) ( x + 1) x + 1. So x 0 is an essential discontinuity, infinite discontinuity, or discontinuity of the second kind. B) using the simplified expression in part (a), predict the shape for the graph of the function 2 x fx x =. These holes are called removable discontinuities. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x. C) graph the function 2 x fx x = on a standard ( 10 10)−. Say for example the game is super mario bros, and jumping in a particular pixel will let you beat the stage in 10 seconds, while missing the jump will let you beat it in 20s.
Suppose you have two polynomials in a fraction: Find the removable discontinuity of the following function: A removable discontinuity has a gap that can easily be filled in, because the limit is the same on both sides. A removable discontinuity is sometimes called a point discontinuity, because the function isn't defined at a single (miniscule point). Note that the given definition of removable discontinuity fails to apply to functions for which and for which fails to exist;

Learn how to define a function at a point of removable discontinuity at which it is not defined, as the limit of the function as x approaches that point, to remove a removable discontinuity and.
Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. A removable discontinuity has a gap that can easily be filled in, because the limit is the same on both sides. In the graphs below, there is a hole in the function at x=a. If a function is not continuous at x = a, but the limit of the function at x = a exists, then f(x) has a removable discontinuity. Learn how to define a function at a point of removable discontinuity at which it is not defined, as the limit of the function as x approaches that point, to remove a removable discontinuity and. B) using the simplified expression in part (a), predict the shape for the graph of the function 2 x fx x =. Suppose you have two polynomials in a fraction: removable discontinuities are characterized by the fact that the limit exists. Follow these steps to identify the removable discontinuity of the above function. removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. That depends on the type of function. So x 0 is an essential discontinuity, infinite discontinuity, or discontinuity of the second kind. The left hand and right hand limits at a point exist, are equal but the function is not defined at this point.
A removable discontinuity is sometimes called a point discontinuity, because the function isn't defined at a single (miniscule point). That depends on the type of function. Find the removable discontinuity of the following function: math\displaystyle \frac{p(x)}{q(x)}/math the first step would be to factor mathq(x)/math. A single point where the graph is not defined, indicated by an open circle.

The function of how much time you spend in the stage depending in what pixel you jump has a removable discontinuity.
We remove the problem here by defining the function at point x = 0 to be the limit: In the next section, we will solve some examples in which we will find the removable discontinuity of a function and plot it on the graph. removable discontinuities are characterized by the fact that the limit exists. removable discontinuities occur when a rational function has a factor with an x that exists in both the numerator and the denominator. Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. The next step would be to check if these factors also appear in. We call such a hole a removable discontinuity. Say for example the game is super mario bros, and jumping in a particular pixel will let you beat the stage in 10 seconds, while missing the jump will let you beat it in 20s. Below is the graph for f ( x) = ( x + 2) ( x + 1) x + 1. So x 0 is an essential discontinuity, infinite discontinuity, or discontinuity of the second kind. That depends on the type of function. Learn how to define a function at a point of removable discontinuity at which it is not defined, as the limit of the function as x approaches that point, to remove a removable discontinuity and. A) simplify the rational expression 2x x and state any values of x where the expression is undefined.
39+ Removable Discontinuity Example Function PNG. That depends on the type of function. Learn how to define a function at a point of removable discontinuity at which it is not defined, as the limit of the function as x approaches that point, to remove a removable discontinuity and. C) graph the function 2 x fx x = on a standard ( 10 10)−. Which of the following functions f has a removable discontinuity at x = x 0?if the discontinuity is removable, find a function g that agrees with f for x ≠ x 0 and is continuous on r. For instance, the function f(x) = (x — 1)^2 / (x — 1) has a limit equal to 0 as x goes to 1, but is not defined at x.